
If students want to find the bisector of a given angle in Geometer’s Sketchpad, they can select the angle and the tool angel bisector in the construction menu and then they automatically get the angle bisector. For example, Geometer’s Sketchpad which is a dynamic geometry program involves tools in the construction menu such as ‘midpoint’, ‘intersection’, and ‘angle bisector’. Thus, using different tools such as compass, straightedge, and dynamic geometry programs might cause some differences in students’ reasoning process in geometric constructions. How students construct geometric figures is directly connected to the development of their geometric reasoning (Köse, Tanışlı, Erdoğan, & Ada, 2012).
Some researchers described geometrical constructions by mentioning the use of compass and straightedge (e.g., Axler & Ribet, 2005 Djorić & Janičić, 2004). According to Lim (1997), geometric construction involves carrying out procedural steps to construct geometric entities such as perpendicular line, parallel line, and angle bisectors using geometrical instruments. Geometric construction was described as “a problem situation in which it is required that a desired figure be drawn with the aid of specified instruments (such as the straightedge and compasses) and using specific given data” (Albrecht, 1952, p.5). Throughout the development of geometry, it was stated that geometric constructions have an important role (Stupel, Oxman, & Sigler, 2014) and it is one of the earliest concepts of mathematics (Kuzle, 2013). To comprehend these processes and the connections among them is necessary for being proficient in geometry (Duval, 1998). State the converse of both your two statements from 10).Geometry which is considered as one of the major concepts in mathematics and mathematics education (Clements & Battista, 1992 NCTM, 2000) involves three cognitive processes construction, reasoning, and visualization (Duval, 1998). (Note: you started with parallel lines!) 11) What about the converses of the two conjectures you listed in 10)? Remember that the converse of a conditional (if-then) statement has the hypothesis and conclusion reversed. 10) Write 2 of the 5 conjectures based on your observations in the chart.

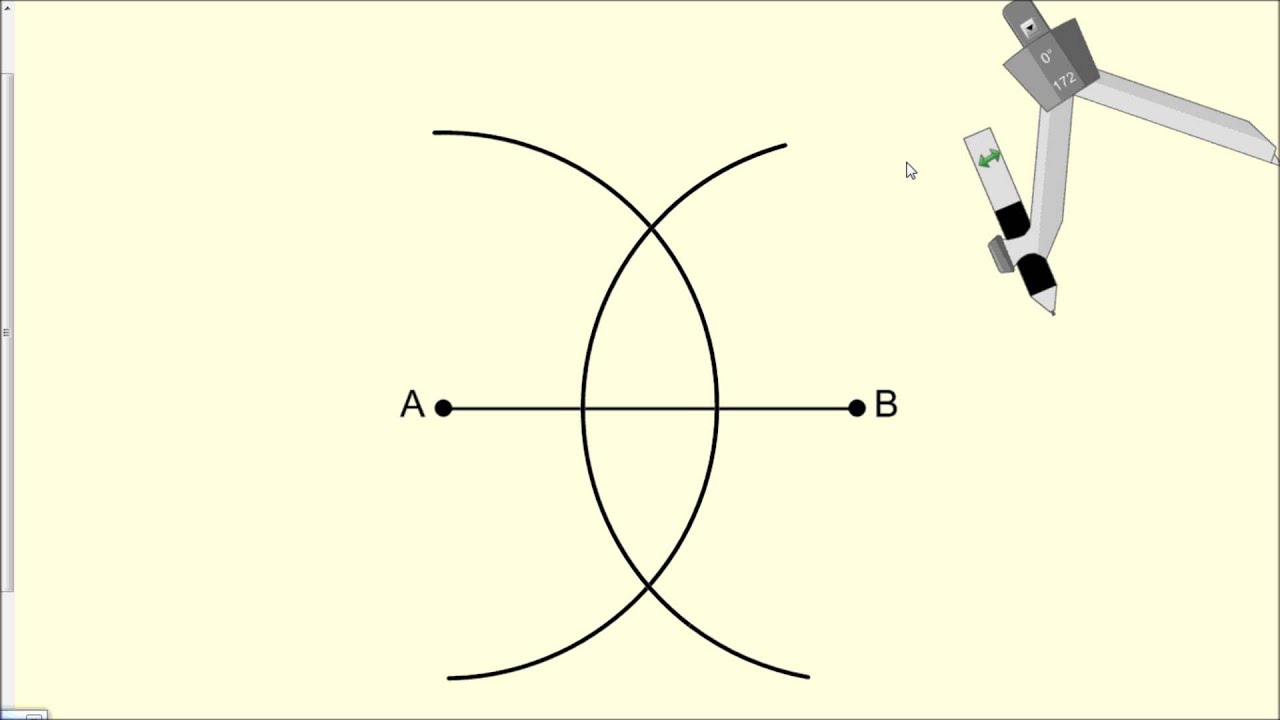
Include a screen shot of your diagram including the measures of the angles and the labels you added. + Angle Type Pair 1 Pair 2 How are they related? (Supplementary or congruent?) Corresponding ZFCE and ZCAB Alternate Interior ZECA and ZCAG Alternate Exterior ZFCE and ZHAG Interior on same side of transversal | ZECA and ZBAC Exterior on same side of transversal ZFCD and ZHAG 9) Use the text feature in Geometer's Sketchpad A to add text to your diagram and label one of the pairs of angles from the chart above. Note: there are more than two pairs of one of these types. 4) What can you say about any point on a segment's perpendicular bisector and its distance to the segment's endpoints?Ĩ) Fill in the chart with other angle pairs of that type and then state how the measures of the pairs of angles are related. What do you notice? (To measure FA: select points F and A, then Measure/Distance.) Step 7: Move point F up and down the line. 2) Can you come up with a shortcut for constructing a perpendicular bisector using the Construct menu? Step 6: Construct a point F on line CD. What is special about point E, the point of intersection? In other words, point E is the of AB. Measure AE and EB (To measure AE: select points A and E, then Measure/Distance.). Investigate: 1) CD is the perpendicular bisector of AB. Select the circles, then Display/Hide Circles or right click on each circle and select Hide Circle. You may either select the line segment and the line and use the construct menu or use the point tool and click on the point of intersection. Step 4: Construct E, the point of intersection of AB and CD. When you click to create points C and D, make sure that both circles highlight which indicates that you are choosing their intersection. (Circle AB means A is the center and AB is the radius Circle BA means B is the center and BA is the radius.) Step 3: Construct CD, where Cand D are the points of intersection of the circles. Sketch: (select New Sketch) Step 1: Construct AB. You should notice that we are replicating Construction 2: Constructing a midpoint of a line segment. Transcribed image text: Investigation: Perpendicular Bisectors In this activity, you'll use only Sketchpad's freehand tools to construct and investigate properties of perpendicular bisectors.


 0 kommentar(er)
0 kommentar(er)
